模板编程（四）：元模板

模板编程

Word count: 2.1kReading time: 9 min

 2024/02/13 

这篇作为模板编程的第四篇，主要讲述一下一些元模板编程的特性。

模板元编程概念

C++ 模板的特性最早是为了支撑泛型，所谓的模板元编程其实是由于意外发现C++ 模板是图灵完备的（Turing-complete)后的一个衍生物。如果C++模板语法可以模拟图灵机的话，那么理论上来说 C++ 模板可以执行任何计算任务，但实际上因为模板是编译期计算，其能力受到具体编译器实现的限制（如递归嵌套深度，C++11 要求最多1024，C++98 要求最多 17）。
C++ 模板元编程是“意外”功能，而不是设计的功能，这也是 C++ 模板元编程语法丑陋的根源。
C++ 模板是图灵完备的，这使得 C++ 成为两层次语言（two-level languages），其中，执行编译计算的代码称为静态代码（static code），执行运行期计算的代码称为动态代码（dynamic code），C++ 的静态代码由模板实现。
具体来说 C++ 模板可以做以下事情：编译期数值计算、类型计算、代码计算（如循环展开），其中数值计算实际不太有意义，而类型计算和代码计算可以使得代码更加通用，更加易用，性能更好（也更难阅读，更难调试，有时也会有代码膨胀问题）。编译期计算在编译过程中的位置请见下图，可以看到关键是模板的机制在编译具体代码（模板实例）前执行。

模板元编程范式

从编程范型（programming paradigm）上来说，C++ 模板是函数式编程（functional programming），它的主要特点是：函数调用不产生任何副作用（没有可变的存储），用递归形式实现循环结构的功能。C++ 模板的特例化提供了条件判断能力，而模板递归嵌套提供了循环的能力，这两点使得其具有和普通语言一样通用的能力（图灵完备性）。
从编程形式来看，模板的“<>”中的模板参数相当于函数调用的输入参数，模板中的 typedef 或 static const 或 enum 定义函数返回值（类型或数值，数值仅支持整型，如果需要可以通过编码计算浮点数），代码计算是通过类型计算进而选择类型的函数实现的（C++ 属于静态类型语言，编译器对类型的操控能力很强）。代码示意如下：

#include <iostream>

template<typename T, int i=1>
class someComputing {
public:
typedef volatile T* retType; // 类型计算
enum { retValume = i + someComputing<T, i-1>::retValume }; // 数值计算，递归
static void f() { std::cout << "someComputing: i=" << i << '\n'; }
};

template<typename T> // 模板特例，递归终止条件
class someComputing<T, 0> {
public:
enum { retValume = 0 };
};

template<typename T>
class codeComputing {
public:
static void f() { T::f(); } // 根据类型调用函数，代码计算
};

int main(){
    someComputing<int>::retType a=0;
    std::cout << sizeof(a) << '\n'; // 64-bit 程序指针
    std::cout << someComputing<int, 500>::retValume << '\n'; // 1+2+...+500
    codeComputing<someComputing<int, 99>>::f();
    std::cin.get(); return 0;
}

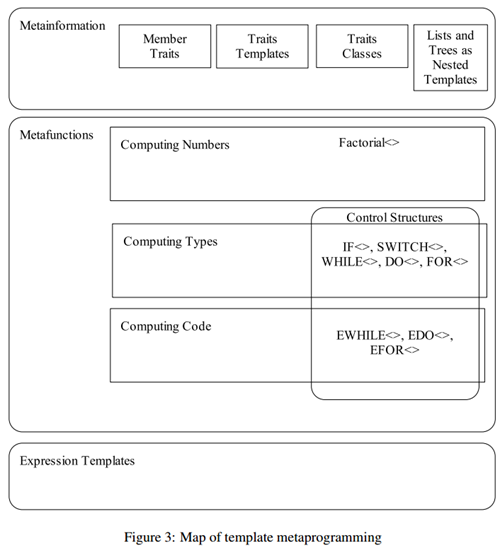
编程的概览图如下：

模板元编程应用

编译期间数值计算

前面已经有了利用模板实现阶乘的示例代码，下面给出一份更简单的用模板实现求和的示例代码来说明模板在编译期间实现数值计算的具体原理。

#include <iostream>

template<int N>
class sumt{
public: static const int ret = sumt<N-1>::ret + N;
};
template<>
class sumt<0>{
public: static const int ret = 0;
};

int main() {
    std::cout << sumt<5>::ret << '\n';
    std::cin.get(); return 0;
}

当编译器遇到 sumt<5> 时，试图实例化之，sumt<5> 引用了 sumt<5-1> 即 sumt<4>，试图实例化 sumt<4>，以此类推，直到 sumt<0>，sumt<0> 匹配模板特例，sumt<0>::ret 为 0，sumt<1>::ret 为 sumt<0>::ret+1 为 1，以此类推，sumt<5>::ret 为 15。值得一提的是，虽然对用户来说程序只是输出了一个编译期常量 sumt<5>::ret，但在背后，编译器其实至少处理了 sumt<0> 到 sumt<5> 共 6 个类型。
从这个例子我们也可以窥探 C++ 模板元编程的函数式编程范型，对比结构化求和程序：for(i=0,sum=0; i<=N; ++i) sum+=i; 用逐步改变存储（即变量 sum）的方式来对计算过程进行编程，模板元程序没有可变的存储（都是编译期常量，是不可变的变量），要表达求和过程就要用很多个常量：sumt<0>::ret，sumt<1>::ret，…，sumt<5>::ret 。函数式编程看上去似乎效率低下（因为它和数学接近，而不是和硬件工作方式接近），但有自己的优势：描述问题更加简洁清晰（前提是熟悉这种方式），没有可变的变量就没有数据依赖，方便进行并行化。

循环展开

部分古早的观点会认为，模板元编程会在循环展开中起到作用，例如一篇早期的测试：
http://web.archive.org/web/20050310091456/http://osl.iu.edu/~tveldhui/papers/Template-Metaprograms/meta-art.html
其中提到了如以下代码以冒泡排序进行的示例：

#include <utility>  // std::swap

// dynamic code, 普通函数版本
void bubbleSort(int* data, int n)
{
    for(int i=n-1; i>0; --i) {
        for(int j=0; j<i; ++j)
            if (data[j]>data[j+1]) std::swap(data[j], data[j+1]);
    }
}
// 数据长度为 4 时，手动循环展开
inline void bubbleSort4(int* data)
{
#define COMP_SWAP(i, j) if(data[i]>data[j]) std::swap(data[i], data[j])
    COMP_SWAP(0, 1); COMP_SWAP(1, 2); COMP_SWAP(2, 3);
    COMP_SWAP(0, 1); COMP_SWAP(1, 2);
    COMP_SWAP(0, 1);
}

// 递归函数版本，指导模板思路，最后一个参数是哑参数（dummy parameter），仅为分辨重载函数
class recursion { };
void bubbleSort(int* data, int n, recursion)
{
    if(n<=1) return;
    for(int j=0; j<n-1; ++j) if(data[j]>data[j+1]) std::swap(data[j], data[j+1]);
    bubbleSort(data, n-1, recursion());
}

// static code, 模板元编程版本
template<int i, int j>
inline void IntSwap(int* data) { // 比较和交换两个相邻元素
    if(data[i]>data[j]) std::swap(data[i], data[j]);
}

template<int i, int j>
inline void IntBubbleSortLoop(int* data) { // 一次冒泡，将前 i 个元素中最大的置换到最后
    IntSwap<j, j+1>(data);
    IntBubbleSortLoop<j<i-1?i:0, j<i-1?(j+1):0>(data);
}
template<>
inline void IntBubbleSortLoop<0, 0>(int*) { }

template<int n>
inline void IntBubbleSort(int* data) { // 模板冒泡排序循环展开
    IntBubbleSortLoop<n-1, 0>(data);
    IntBubbleSort<n-1>(data);
}
template<>
inline void IntBubbleSort<1>(int* data) { }

我复现了该程序，并且使用了如下代码进行测试：

int main() {
    const int num=100000000;
    int data[4]; int inidata[4]={3,4,2,1};
    auto t1 = std::chrono::high_resolution_clock::now();
    for(int i=0; i<num; ++i) { memcpy(data, inidata, 4); bubbleSort(data, 4); }
    std::chrono::duration<double, std::milli> t1_cost = std::chrono::high_resolution_clock::now() - t1;
    auto t2 = std::chrono::high_resolution_clock::now();
    for(int i=0; i<num; ++i) { memcpy(data, inidata, 4); bubbleSort4(data); }
    std::chrono::duration<double, std::milli> t2_cost = std::chrono::high_resolution_clock::now()-t2;
    auto t3 = std::chrono::high_resolution_clock::now();
    for(int i=0; i<num; ++i) { memcpy(data, inidata, 4); IntBubbleSort<4>(data); }
    std::chrono::duration<double, std::milli> t3_cost = std::chrono::high_resolution_clock::now()-t3;

    std::cout << "迭代/模板 = " <<t1_cost/t3_cost << '\t' << "迭代展开/模板 = " <<t2_cost/t3_cost << '\n';
    std::cin.get();
    return 0;
}